X(3333)
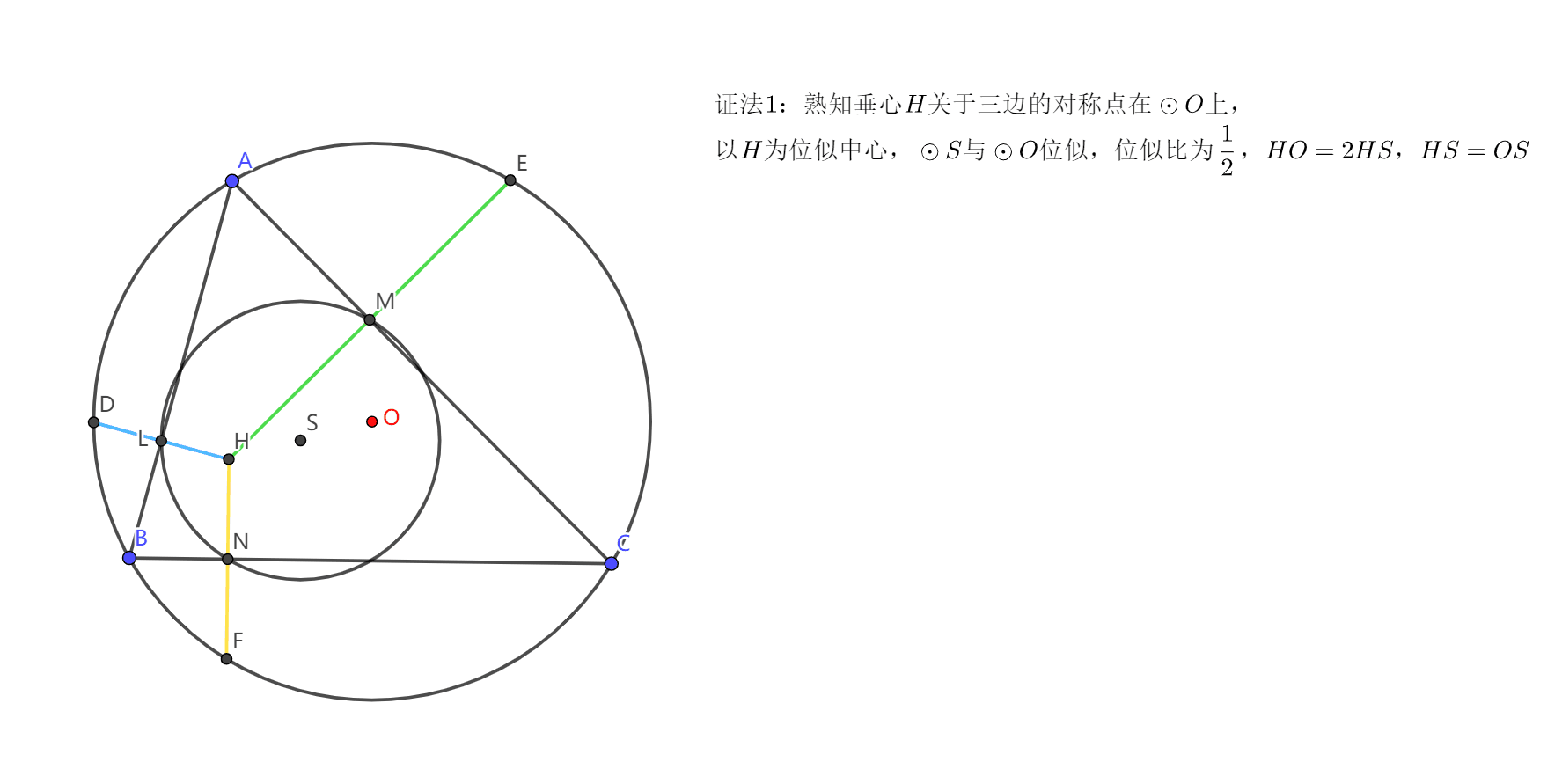
关于\(X(3333)\)存在性的证明
\[
\begin {aligned}
\triangle IBC, \triangle IAC ,& \triangle IAB的共轭重心为K_A,K_B,K_C
, IA,IB,IC的中点为M_A,M_B,M_C \\
& K_AM_A,K_BM_B,K_CM_C,OI共点于X(3333)
\end {aligned}
\] /desc.svg)
Lemma 1
\(\omega _A,\omega _B, \omega
_C\)为三个伪内切圆, 切\(\odot
O\)于\(T_A,T_B,T_C\) \(AT_A,BT_B,CT_C\)三线共点 /Lemma1.svg)
Proof
设\(K\)为\(\odot O\)于\(\odot I\)的位似中心. 对\(\odot I\),\(\odot O\),\(\omega _A\)使用蒙日定理得\(A,K,T_A\)共线 同理可得\(AT_A,BT_B,CT_C\)三线共点
Lemma 2
\(\triangle A_1B_1C_1\)为内切三角形,\(\triangle I_AI_BI_C\)为旁心三角形他们的位似中心\(K\)在\(OI\)上
/Lemma2.svg)
Proof
由于\(I_AA\perp I_BI_C\) 因此\(I\) 为\(\triangle I_A I_B I_C\)的垂心,
取\(N\)为\(I_B I_C\)与\(\odot (ABC)\)的第二交点,易知N为北极点,由鸡爪定理知\(N\)为\(I_BI_C\)中点,
因此\(O\)为\(\triangle I_AI_BI_C\)的九点圆圆心
取\(I\)关于\(O\)的对称点\(P\)为\(,P\)为\(\triangle I_AI_BI_C\)的外心,显然\(I\)为\(\triangle A_1 B_1C_1\)的外心
因为\(B_1C_1 \parallel I_B I_C\)因此\(\triangle A_1 B_1C_1\)与\(\triangle I_AI_BI_C\)位似
由于位似对应,\(K,I,P\)共线,即\(K,I,O\)共线
Lemma 3
\(N\),\(S\)为南,北极点,\(D=NI \cap BC\),\(\triangle A_1B_1C_1\)为内切三角形,\(A_1\)在\(B_1C_1\)的投影为\(P\)
则\(A,P,D\)共线
/Lemma3.svg)
Proof
\(\angle IA_1N=\frac{\pi}{2}-\angle NA_1C=\frac{\pi}{2}-\angle NEC-\angle BEC=\angle CES - \angle BAE=\angle EAI\),因此\(\odot(AIA_1S)\)
取\(BC\)与\(\odot AIA_1S\)第二交点\(F\),\(\odot BIC\)与\(\odot AIA_1S\)第二交点\(G\)
重新定义\(D=AE\cap BC\),只需证\(N\in DG,P \in AE\)
$IAF = IA_1F = = NAS F,A,N $共线
\(\angle AFA_1=\angle AEA_1 = \angle ACN \implies \triangle NCA \sim \triangle NFC\)
\(NA \cdot NF = NC^2 \implies N\in \odot AIA_1S,\odot (BIC)\)的根轴\(GI\)
由根心定理\(GIN,BC,AE\)共点于\(D \implies D \in GN\)也即\(N\in DG\)
熟知\(\triangle PC_1B \sim \triangle PB_1C \implies \frac{PC_1}{PB_1}=\frac{BC_1}{CB_1}=\frac{BA_1}{CA_1}\)
又因为\(\triangle AB_1C_1 \sim \triangle NCB\),由上\(P,A_1\)为相似对应点,
因此\(\triangle AB_1P \sim \triangle NCA_1\),\(\angle PAB_1 = \angle A_1NC=\angle EAC \implies P \in AE\)
下面我们就可以开始对主命题证明啦
我们的主要思路是构造三个特征点,用这三个点及调和关系去框定X(3333)
/p1.svg)
/p2.svg)
## 性质
